I've done a number of postings on programming OpenGL ES for the iPhone, but most of the posts I've done have been targeted at people who already know at least a little bit about 3D programming.
If you haven't already done so, grab a copy of my Empty OpenGL Xcode project template. We'll use this template as a starting point rather than Apple's provided one. You can install it by copying the unzipped folder to this location:
/Developer/Platforms/iPhoneOS.platform/Developer/Library/Xcode/Project Templates/Application/There are a number of good tutorials and books on OpenGL. Unfortunately, there aren't very many on OpenGL ES, and none (at least as I write this) that are specifically designed for learning 3D programming on the iPhone. Because most available material for learning OpenGL starts out teaching using what's called direct mode, which is part of the functionality of OpenGL that's not in OpenGL ES, it can be really hard for an iPhone dev with no 3D background to get up and running using existing books and tutorials. I've had a number of people request it, so I've decided to start a series of blog posts designed for the absolute 3D beginner. This is the first in that series. If you've read and understood my previous OpenGL postings, you will probably find this series to be a little too basic.
OpenGL Datatypes
The first thing we'll talk about are OpenGL's datatypes. Because OpenGL is a cross-platform API, and the size of datatypes can vary depending on the programming language being used as well as the underlying processor (64-bit vs. 32-bit vs 16-bit), OpenGL declares its own custom datatypes. When passing values into OpenGL, you should always use these OpenGL datatypes to make sure that you are passing values of the right size or precision. Failure to do so could cause unexpected results or slowdowns caused by data conversion at runtime. Every implementation of OpenGL, regardless of platform or language, declares the standard OpenGL datatypes in such a way that they will be the same size on every platform, making porting OpenGL code from one platform to another easier.
Here are the OpenGL ES datatypes:
- GLenum: An unsigned integer used for GL-specific enumerations. Most commonly used to tell OpenGL the type of data stored in an array passed by pointer (e.g. GL_FLOAT) to indicate that the array is made up of GLfloats.
- GLboolean: Used to hold a single boolean values. OpenGL ES also declares its own true and false values (GL_TRUE and GL_FALSE) to avoid platform and language differences. When passing booleans into OpenGL, use these rather than YES or NO (though it won't hurt if you accidentally use YES or TRUE since they are actually defined the same. But, it's good form to use the GL-defined values.
- GLbitfield: These are four-byte integers used to pack multiple boolean values (up to 32) into a single variable using bitwise operators. We'll discuss this more the first time we use a bitfield variable, but you can read up on the basic idea over at wikipedia
- GLbyte: A signed, one-byte integer capable of holding a value from -128 to 127
- GLshort: A signed two-byte integer capable of holding a value between −32,768 to 32,767
- GLint: A signed four-byte integer capable of holding a value between −2,147,483,648 and 2,147,483,647
- GLsizei: A signed, four-byte integer used to represent the size (in bytes) of data, similar to size_t in C.
- GLubyte: An unsigned, one-byte integer capable of holding a value between 0 and 255.
- GLushort: An unsigned, two-byte integer capable of holding a value between 0 and 65,535
- GLuint: An unsigned, four-byte integer capable of holding a value between 0 and 4,294,967,295
- GLfloat: A four-byte precision IEEE 754-1985 floating point variable.
- GLclampf: This is also a four-byte precision floating point variable, but when OpenGL uses GLclampf, it is indicating that the value of this particular variable should always be between 0.0 and 1.0.
- GLvoid: A void value used to indicate that a function has no return value, or takes no arguments.
- GLfixed: Fixed point numbers are a way of storing real numbers using integers. This was a common optimization in 3D systems used because most computer processors are much faster at doing math with integers than with floating-point variables. Because the iPhone has vector processors that OpenGL uses to do fast floating-point math, we will not be discussing fixed-point arithmetic or the GLfixed datatype.
- GLclampx: Another fixed-point variable, used to represent real numbers between 0.0 and 1.0 using fixed-point arithmetic. Like GLfixed, we won't be using or discussing this datatype.
OpenGL ES (at least the version used on the iPhone) does not support any 8-byte (64-bit) datatypes such as long or double. OpenGL does have these larger datatypes, but given the screen size of most embedded devices, and the types of applications you are likely to be writing for them, the decision was made to exclude them from OpenGL ES under the assumption that there would be little need for them, and that their use could have a detrimental effect on performance.
The Point or Vertex
The atomic unit in 3D graphics is called the point or vertex. These represent a single spot in three dimensional space and are used to build more complex objects. Polygons are built out of these points, and objects are built out of multiple polygons. Although regular OpenGL supports many types of polygons, OpenGL ES only supports the use of three-sided polygon, (aka triangles).
If you remember back to high-school geometry, you probably remember something called Cartesian Coordinates. The basic idea is that you select an arbitrary point in space and call it the origin. You can then designate any point in space by referencing the origin and using three numbers, one for each of the three dimensions, which are represented by three imaginary lines running through the origin. The imaginary line running from left to right is called the x-axis. Traveling along the x-axis, as you go to the right along the x axis, the value gets higher and as you go to the left, they get lower. Left of the origin are negative x values, and to the right are positive x values. The other two axes work exactly the same way. Going up along the y axis, the value of y increases, and going down, it decreases. Values above the origin have a positive y value, and those below the origin have a negative y value. With z, as objects move away from the viewer, the value gets lower, and as they move toward the viewer (or continue behind the viewer), values get higher. Points that are in front of the origin have a positive z value, and those that are behind the origin have a negative z value. The following illustration might make help those words make a little more sense:
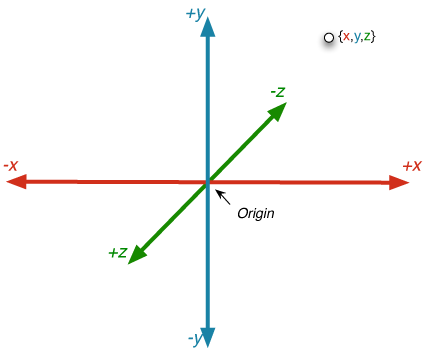
Note: Core Graphics, which is another framework for doing graphics on the iPhone uses a slightly different coordinate system in that the y axis decreases as it goes up from the origin, and increases as it goes down.
The value that increases or decreases along these axes are in an arbitrary scale - they don't represent any real measurement, like feet, inches, or meters. You can select any scale that makes sense for your own programs. If you want to design a game where each unit is a foot, you can do that. if you want to make each unit a micron, you can do that as well. OpenGL doesn't care what they represent to the end user, it just thinks of them as units, and make sure they are all equal distances.
Since any object's location in three-dimensional space can be represented by three values, an object's position is generally represented in OpenGL by the use of three GLfloat variables, usually using an array of three floats, where the first item in the array (index 0) is the x position, the second (index 1) is the y position, and the third (index 2) is the z position. Here's a very simple example of creating a vertex for use in OpenGL ES:
GLfloat vertex;
vertex = 10.0; // x
vertex = 23.75; // y
vertex = -12.532; // zIn OpenGL ES, you generally submit all the vertices that make up some or all of the objects in your scene as a vertex array. A vertex array is simply an array of values (usually GLfloats) that contains the vertex data for some or all of the objects in the world. We'll see how that process works in the next post in this series, but the thing to remember about vertex arrays is that their size is based on the number of vertices being submitted multiplied by either three (for drawing in three-dimensional space) or two (for drawing in two-dimensional space). So, a vertex array that holds six triangles in three-dimensional space would consist of an array of 54 GLfloats, because each triangle has three vertices, and each vertex has three coordinates and 6 x 3 x 3 = 54.
Dealing with all these GLfloats can be a pain, however, because you're constantly having to multiply things in your head and try to think of these arrays in terms of the vertices and polygons that they represent. Fortunately, there's an easier way. We can define a data structure to hold a single vertex, like this:
typedef struct Vertex3D;
By doing this, our code becomes much more readable:
Vertex3D vertex;
vertex.x = 10.0;
vertex.y = 23.75;
vertex.z = -12.532;Now, because our Vertex3D struct is comprised of three GLfloats, passing a pointer to a Vertex3D is exactly the same as passing a pointer to an array of three GLfloats. There's no difference to the computer; both have the same size and the same number of bytes in the same order as OpenGL expects them. Grouping the data into these data structures just makes it easier for us as the programmer to visualize and deal with the data. If you download my Xcode template from the beginning of this article, this data structure and the supporting functions I'm going to be discussing next have already been defined in the file named OpenGLCommon.h. There is also an inline function for creating single vertices:
static inline Vertex3DIf you remember back to geometry (or maybe you don't, which is okay), the distance between two points on a plane is calculated using this formula:
We can implement this formula to calculate the straight-line distance between any two points in three-dimensional space with this simple inline function:
static inline GLfloat;Triangles
Since OpenGL ES only supports triangles, we can also create a data structure to group three vertices into a single triangle object.
typedef struct Triangle3D;Again, a single Triangle3D is exactly the same as an array of nine GLfloats, it's just easier for us to deal with it in our code because we can build objects out of vertices and triangles rather than out of arrays of GLfloats.
There are a few more things you need to know about triangles, however. In OpenGL, there is a concept known as winding, which just means that the order in which the vertices are drawn matters. Unlike objects in the real world, polygons in OpenGL do not generally have two sides to them. They have one side, which is considered the front face, and a triangle can only be seen if its front face if facing the viewer. While it is possible to configure OpenGL to treat polygons as two-sided, by default, triangles have only one visible side. By knowing which is the front or visible side of the polygon, OpenGL is able to do half the amount of calculations per polygon that it would have to do if both sides were visible.
Although there are times when a polygon will stand on its own, and you might very well want the back drawn, usually a triangle is part of a larger object, and one side of the polygon will be facing the inside of the object and will never be seen. The side that isn't drawn is called a backface, and OpenGL determines which is the front face to be drawn and which is the backface by looking at the drawing order of the vertices. The front face is the one that would be drawn by following the vertices in counter-clockwise order (by default, it can be changed). Since OpenGL can determine easily which triangles are visible to the user, it can use a process called Backface Culling to avoid doing work for polygons that aren't facing the front of the viewport and, therefore, can't be seen. We'll discuss the viewport in the next posting, but you can think of it as the virtual camera, or virtual window looking into the OpenGL world.

In the illustration above, the cyan triangle on the left is a backface and won't be drawn because the order that the vertices would be drawn in relation to the viewer is clockwise. On the other hand, the triangle on the right is a frontface that will be drawn because the order of the vertices is counter-clockwise in relation to the viewer.
In the next posting in this series, we'll look at setting up the virtual world in OpenGL and do some simple drawing using Vertex3D and Triangle3D. In the post after that, we'll look at transformations which are a way of using linear algebra to move objects around in the virtual world.



 10:17 AM
10:17 AM
 Unknown
Unknown

 Posted in:
Posted in: 


0 nhận xét:
Post a Comment